CRC (Cyclic Redundancy Check)

I'm not gonna talk about definitions here. It has been well documented, well, millions of times I guess. What I'm going to talk about here is the logic behind CRC and why certain arithmetic approach is adopted to calculate CRC.

What is XOR

Still not a definition. Come to think about what XOR does is to find out the difference between two entities. And entity may be a number, may be a frame transmit through network. For clarification, I borrowed the picture from accu.org (full url can be found in reference, I really recommend everybody to read it) to show XOR's capability.

This is what logic AND does, to find the same part which is the intersection.

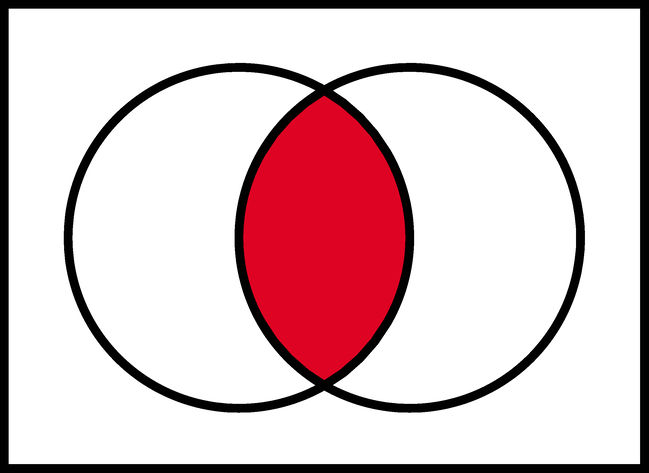
This is what OR does. To find the union of two entity. It's an either...or... situation where you pick whatever is available.

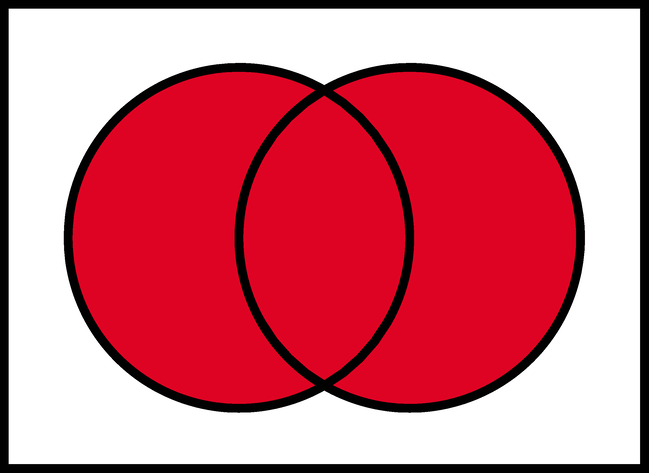
And this is for XOR. As mentioned above, it is to find the difference between the two circles, or entities, or sets, name it whatever.

You know how to efficiently swap two numbers.

a = a ^ b;

b = a ^ b;

a = a ^ b;

This can be think of like this.

First find the difference between a and b and store the difference in a.

Then, search in every bit of b with the difference bits, cut them out and store the result in b. What's b without the difference with a, it's a. So a is swapped into variable b now.

The last step, bear in mind that the value in variable b is a, find out all the different bits in a (those different from b), and cut them out, what's left is the value of b.

Two numbers are swapped.

Why XOR

It is really counter intuitive first time I read about the bytes and bits behind XOR. This is so fascinating about the computer world that things are going to melt your brain, at any moment. You never know. You stay foolish.

Right back at the topic. To answer why utilize XOR in CRC is pretty simple. Because CRC is designed to check if the frame received is identical to the one sent. Another saying would be, to find the difference between any one bit that's been altered or tampered that cause the final frame different from the one sent (CRC is only good for one-bit-incorrect only,  need to work on this later).

As mentioned before, XOR is capable of finding the difference between two entities, thus it is what we look for.

Now, to further understand how CRC works. Some concepts should be talked about.

Frame Check Sequence

The Frame Check Sequence, or FCS, will be appended to the end of transmitting message to check if the message is corrupted.

As we'll see later, the FCS is calculated with Modulo 2 Arithmetic and the length of FCS is corresponding to the highest polynomial degree of the generating polynomial, which all of them will be discussed below.

Modulo 2 Arithmetic

XOR has this Modulo-2 arithmetic explanation. And modulo 2 arithmetic is used in final calculation of the FCS (Frame Check Sequence).

Blah! First things first. Let's come to see the theory, then explain them a bit.

Addition Equals to Subtraction Equals to XOR

In modulo 2 arithmetic, addition is equal to subtraction and , is equal to the result of XOR. HA!

Rules for addition:

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1 = 0

This is pretty basic, since the result is the same as applying XOR on the two bits.

Now, if 1 + 1 = 0, then 0 - 1 = 1, which we can deduce. Hence,

0 - 0 = 0

0 - 1 = 1

1 - 0 = 1

1 - 1 = 0

Pretty interesting! Now, mark this in mind. Subtraction is addition, which is XOR.

Polynomial Representation of Data

Think of the data we want to transmit as 111010, the data can be represented by 1 * x^5 + 1* x^4 + 1 * x^3 + 0 * x^2 + 1 * x^1 + 0 * x^0, hence x^5 + x^4 + x^3 + x.

The power starts with 0 from the least significant bit all the way to the most significant bit. This is also true with generating polynomial.

Generating Polynomial

The generating polynomial can be seen as a "key" to calculate the FCS.

For example, consider 11001 is the generating polynomial for calculating FCS when sending data 111010. Then, the length of final calculated FCS will be 4 bits long. Since the highest polynomial degree of the generating polynomial is 4 (x^4 + x^3 + 1).

Generating polynomial can be any bits, but there're certain best practices to follow. Check it out here!

Long Division

Long division is the last step in calculating FCS. It requires the same bits be selected from the data starting with the highest bits, to do an XOR or subtraction with the generating polynomial. If the length is not long enough to match the generating polynomial, then a 0 is added to the result. Otherwise, it is a 1. Keep doing this until you have no bits left in the data, then the remainder left-padded with enough 0 to match the length of the highest polynomial degree of the generating polynomial is the final FCS to be appended to the data, and send to the recipient.

Video Link

I'm not going to show the actual steps in calculating the FCS. Here is the video tutorial to calculate it. It's well explained.

Final Thoughts

Just another interesting bit I encountered when reading TCP/IP Volume 1. XOR has lots of applications, read the article in the first reference link. It's good.

References

https://accu.org/journals/overload/20/109/lewin_1915/

http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.5.5027&rep=rep1&type=pdf